2.3.2. Термические коэффициенты

Взаимосвязь свойств однородного вещества в равновесном состоянии может также характеризоваться термическими коэффициентами. Эти коэффициенты могут быть определены опытным путем, они имеют определенный физический смысл.

Взаимосвязь термических коэффициентов можно получить, используя уравнение состояния вещества в явном виде Р=F(v,T), представив его в виде полного дифференциала

(2.14)

приняв Р = const, получим

преобразовав это выражение, получим соотношение вида:

(2.15)

В выражении (2.15) отношение (dv/dP)_Т характеризует интенсивность изменения объема в зависимости от изменения давления при постоянной температуре. Отношение этой величины к удельному объему v₀, взятому при фиксированном состоянии (например, при нормальных условиях) с обратным знаком называется коэффициентом изотермической сжимаемости, и обозначается как μ

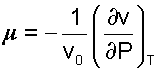(2.16)

Отношение (dv/dТ)_Р характеризует интенсивность изменения объема в зависимости от изменения температуры при постоянном давлении. Разделив его на v₀, получим коэффициент изобарного расширения, обозначающийся как α

(2.17)

Отношение (dР/dТ)_V характеризует изменение давления в зависимости от изменеия температуры при постоянном объеме. Разделив его на Р₀, получим коффициент упругости, обозначающийся как β

(2.18)

Выразив значения частных производных в выражении (2.15) через термические коэффициенты (dv/dP)_T = - μ v₀ , (dv/dТ)_P = α v₀ , (dР/dТ)_V = β P₀ , и подставив их в (2.15), получим уравнение взаимосвязи термических коэффициентов

(2.19)

Выражение (2.19), как и уравнение состояния, описывает свойства вещества. Кроме этого, выражение (2.19) необходимо для расчета коэффициента β твердых и жидких тел, поскольку эти тела невозможно нагреть без изменения их объема, т.е. β для них опытным путем определить невозможно.