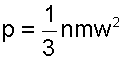
(4.1)
Газы часто используются в тепловых двигателях в качестве рабочего тела. Это обусловлено их свойством менять объем в широком диапазоне, и, следовательно, получать работу расширения. Знать свойства газов очень важно, т.к. необходимо анализировать процессы, проходящие с рабочим телом в установках и выбирать наиболее экономичные схемы (циклы) этих установок.
Изучение свойств газов ведется двумя путями: экспериментальным и теоретическим. На начальной стадии изучения свойств газов преобладали экспериментальные исследования. В настоящее время теоретические и экспериментальные исследования проводятся совместно. Подтверждение всех теорий возможно только опытным экспериментом.
Теоретическое изучение свойств газов ведется сначала на упрощенной их модели - идеальном газе.
Под идеальным газом понимается газ, в котором отсутствуют силы гравитационного взаимодействия между молекулами, образующими газ, а механическое взаимодействие молекул ограничено лишь упругим соударением, сами молекулы при этом представляют идеально упругие материальные точки, не имеющих объема.
В соответствии с определением идеального газа, поведение молекул в нем подчиняется законам механики. Созданная на основании этих законов теория идеальных газов получила название молекулярно-кинетической теории идеальных газов.
В соответствии с этой теорией абсолютное давление идеального газа определяется исходя из закона импульсов [7], и рассчитывается как
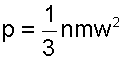 |
(4.1) |
В соответствии с определением абсолютного давления, давление идеального газа соответствует силовому воздействию его молекул друг на друга или на окружающую их поверхность, на единицу площади и направленно по нормали к этой поверхности. Величина 1/3 в выражении (4.1) указывает на то, что силовое воздействие молекул идеального газа равномерно распределено по всем степеням свободы поступательного движения молекул (у поступательного движения 3 степени свободы). Это объясняется тем, что число молекул даже в малом объеме очень велико, а их движение хаотично.
Ранее было показано, что кинетическая энергия поступательного движения молекул прямо пропорциональна величине абсолютной температуры газа
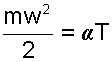 |
Воспользовавшись этим соотношением, запишем выражение (4.1) в виде
 |
(4.2) |
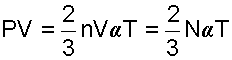 |
(4.3) |
Исходя из выражения (4.3) можно сделать следующие заключения:
1) При одинаковых физических условиях (Р и Т одинаковы) в одинаковых объемах (V=idem) находится одинаковое количество молекул идеальных газов N=idem, независимо от того какой газ или смесь газов заполняет данный объем;
2) Поскольку масса однородного газа равна произведению массы одной молекулы на число молекул, то в соответствии с заключением 1, плотность идеальных газов ρ при одинаковых Р и Т пропорциональна их молекулярной массе μ
 |
(4.4) |
Последнее соотношение выражения (4.4) относится к объему одного моля (киломоля) газа μv [м3/кмоль], где μ [кг/кмоль] - молярная масса газа. Использование киломоля, а не моля объясняется тем, что все расчетные выражения принято давать в системе СИ (масса в кг, объем в м3 и т.п.).
В результате второе заключение можно сформулировать так: объем одного киломоля (моля) идеальных газов, имеющих одинаковые Р и Т одинаков. Обозначив объем одного киломоля газа величиной Vμ = μv, получим
3) Записав выражение (4-3) для одного киломоля газа, получим соотношение
 |
(4.5) |
Применив два предыдущих заключения к выражению (4.5), получим, что при одинаковых Р и Т один киломоль идеального газа занимает одинаковый объем и содержит в этом объеме одинаковое количество молекул. Следовательно, согласно закону сохранения вещества, количество молекул в киломоле всех идеальных газов при изменении Р и Т не изменится, т.е. это величина постоянная Nμ=const.
Несложно догадаться, что все три заключения представляют собой закон Авогадро, а величина Nμ=6,0236·1026 [1/кмоль], есть число Авогадро.
В выражении (4.5) произведение (2/3) Nμα есть постоянная величина для всех идеальных газов. Эту константу обозначили как Rμ и назвали универсальной газовой постоянной.
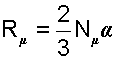 |
(4.6) |
Определение универсальной газовой постоянной было осуществлено экспериментально на газах при малых значениях давлений. При малых давлениях расстояние между молекулами газа очень большие, силы межмолекулярного взаимодействия практически отсутствуют, а свойства реальных газов близки к свойствам идеальных газов. Известно, что при нормальных физических условиях P0=760 мм рт.ст.=101325 Па и Т0=273,15 К один киломоль всех газов занимает объем Vμ0=22,4 [м3/кмоль]. Подставив эти параметры в уравнение (4.5) получим численное значение универсальной газовой постоянной и ее размерность [Дж/(кмоль·K]
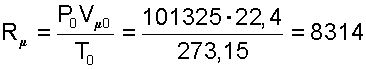 |
В окончательном виде уравнение (4.5) можно записать в следующих представлениях:
для киломоля газа
(4.7) |
поделив правую и левую часть уравнения (4.7) на молярную массу μ, получим уравнение для одного килограмма газа
 |
(4.8) |
v - удельный объем газа в м3/кг;
умножив правую и левую части уравнения (4.8) на массу m, получим уравнение для m килограммов газа
(4.9) |
Все три уравнения (4.7), (4.8), (4.9) являются уравнением состояния идеального газа, выражающие взаимосвязь термических параметров состояния: Р, v (V или Vμ), T. Эти уравнения называются термическим уравнением состояния идеального газа или по их авторам - уравнением Менделеева - Клапейрона.
Состояние идеального газа определяется любой парой термических параметров из трех Р, v, T. Третий параметр может быть определен из термического уравнения состояния идеального газа.
Уравнение состояния идеального газа было получено в 1834 г. Клапейроном для одного килограмма газа (4.8), а в 1874 г. Менделеевым для одного моля газа (4.7). Уравнение состояния идеального газа было получено на основании экспериментальных закономерностей, полученных в ХVII-XIX веках учеными, исследовавшими свойства газов при параметрах, близких к комнатным:
- закон Бойля-Мариотта для Т=const Pv=const,Эти законы являются частными случаями уравнения состояния идеального газа и легко могут быть получены из него.
| предыдущий параграф | содержание | следующий параграф |