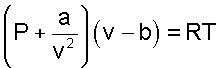
(6.1)
Получение уравнения состояния реального газа, достаточно точно описывающего его термодинамические свойства, очень важная задача. Термические уравнения состояния используются не только для расчета термических параметров и их изменений, но и для определения энергетических (калорических) величин и теплоемкостей (u, h, s, cP, cV и т.п.) с помощью дифференциальных уравнений термодинамики.
Одним из первых попытку получить уравнение состояния, описывающее свойства вещества в газообразном и жидком видах, предпринял в 1887 году голландский ученый Ван-дер-Ваальс [10]. Основываясь на логических рассуждениях, он составил уравнение
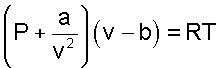 |
(6.1) |
где a и b - постоянные величины, так же как и R характеризующие индивидуальные свойства вещества.
Уравнение Ван-дер-Ваальса отличается от уравнения Клапейрона тем, что вместо давления Р в нем фигурирует сумма (Р + a/v2), а вместо объема v стоит разность (v - b).
Ван-дер-Ваальс на основании простейших молекулярно-кинетических соображений показал, что силы взаимного притяжения молекул обратно пропорциональны квадрату удельного объема v, следовательно, членом a/v2 учитывается взаимодействие молекул газа. Из физики известно, что силы взаимного притяжения молекул приводят к появлению внутреннего давления в газах и жидкостях, следовательно, величину a/v2 можно рассматривать как внутреннее давление газа.
Согласно уравнению Клапейрона для изотермического процесса при Р→∞ v→0. Из уравнения Ван-дер-Ваальса следует, что при давлении Р→∞ удельный объем v→b, следовательно, величину b можно рассматривать как объем, занимаемый собственно молекулами.
Величины a и b могут определяться экспериментально, но можно их и рассчитать. По расчетам получается, что они зависят от параметров критической точки газа, поэтому газ, подчиняющийся уравнению 5.1, называют ван-дер-ваальсовским газом. Изотермы Ван-дер-Ваальса в Р,v- диаграмме изображены на рис. 6.6. Сверхкритические изотермы качественно соответствуют изотермам реального газа. Докритические изотермы вместо горизонтального участка, характеризующего фазовый переход жидкость-пар, имеют волнообразный участок.
Как показывают расчеты, попытки применения этого уравнения для описания областей, где вещество обладает резко выраженными свойствами реального газа (вблизи линии насыщения и околокритическая область) и тем более области жидкости, приводят к большим отклонениям от реальных значений параметров веществ. Поэтому практическое применение уравнение Ван-дер-Ваальса может найти только в ограниченной области состояний реальных газов [1, 2]. Ценность этого уравнения заключается в возможности качественной оценки и наглядной иллюстрации влияния простейших признаков реального газа на его термодинамические свойства.
В целях усовершенствования уравнения Ван-дер-Ваальса в него вводились поправки. В результате учеными был получен ряд новых уравнений состояния реальных газов. Некоторые из них довольно точно описывали экспериментальные данные и были использованы для составления таблиц термодинамических свойств ряда веществ.
| предыдущий параграф | содержание | следующий параграф |