8.2. Характеристики атмосферного влажного воздуха

При температурах атмосферного воздуха 0-50 ⁰С парциальное давление водяного пара очень мало (0,006-0,07 бар), что позволяет применить к перегретому и сухому насыщенному водяному пару уравнение идеального газа:

(8.3)

(8.4)

Разделив эти выражения друг на друга, получим расчетное выражение относительной влажности воздуха через парциальные давления водяного пара:

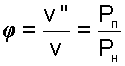(8.5)

Молярная масса атмосферного влажного воздуха определяется по уравнению для смеси газов:

(8.6)

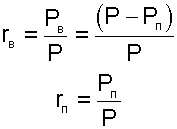В результате подстановки численных значений молярных масс сухого воздуха и водяного пара в выражение (8.6) получаем расчетное выражение молярной массы влажного воздуха в виде:

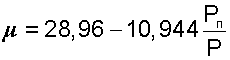(8.7)

Молярная масса влажного воздуха меньше молярной массы сухого воздуха.

Газовая постоянная влажного воздуха определяется выражением:

(8.8)

Плотность влажного воздуха определяется выражением:

(8.9)

Влагосодержание d - это масса водяного пара в граммах, приходящаяся на 1 кг сухого воздуха. В общем случае понятие "влагосодержание" относится не только к паровой фазе воды, но и к жидкой, и к твердой ее фазам. Расчетное выражение для влагосодержания паровой фазы воды в воздухе (г/кг с.в.) получается из соотношения:

(8.10)

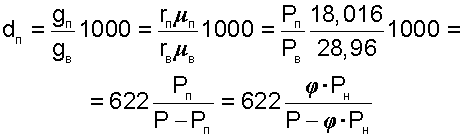(8.11)

Энтальпия влажного воздуха Н рассчитывается на  1 кг сухого воздуха (кДж/кг с.в.) и определяется как сумма энтальпий компонентов, находящихся в 1 кг сухого воздуха:

(8.12)

В выражении (8.12) энтальпии всех компонентов влажного воздуха необходимо подставлять при одинаковых давлениях и температурах начала их отсчета.

Для атмосферного влажного воздуха удельные энтальпии всех компонентов можно рассчитать, приняв ряд допущений, которые не приведут к погрешностям инженерных расчетов в диапазоне изменения атмосферного давления и температуры от -40 до 150 ⁰С более чем на 0,5 %.

Эти допущения сводятся к следующему. Начало отсчета удельной энтальпии сухого воздуха принимают при t₀=0 ⁰С и считают, что энтальпия сухого воздуха зависит только от температуры (как для идеального газа), а его изобарная теплоемкость - величина постоянная. Расчетное выражение удельной энтальпии сухого воздуха в этом случае будет соответствовать соотношению

(8.13)

При таких допущениях удельная энтальпия сухого воздуха (кДж/кг) численно равна его температуре в градусах Цельсия:

Для определения энтальпии воды и водяного пара начало отсчета внутренней энергии u₀ = 0 принято при параметрах тройной точки воды t₀=0,01 ⁰С и Р₀=611,2 Па на линии насыщения х=0. При этих параметрах численное значение энтальпии h₀' = P₀v₀' = 0,000611 кДж/кг представляет очень малую величину, которую для наших расчетов можно принять равной нулю. Таким образом, можно считать, что начало отсчета энтальпии H₂О, как и сухого воздуха, ведется от 0 ⁰С и ее численное значение при этой температуре равно нулю (h_П0=0).

Для дальнейшего пояснения определения энтальпии водяного пара рассмотрим изобару Р₀, соответствующую тройной точке воды в Т,s- диаграмме (рис.8.2). Площадь ЕС11'0Е под изобарой Е-1 представляет в T,s- диаграмме теплоту изобарного процесса, состоящую из теплоты парообразования и теплоты перегрева пара, которая рассчитывается как разница энтальпий:

Поскольку энтальпию в тройной точке воды (точка Е) мы приняли за нуль, то абсолютное значение удельной энтальпии пара в точке 1 определяется выражением

Приняв изобарную теплоемкость перегретого пара величиной постоянной, c_РП=1,93 кДж/(кг К), что допустимо для интервала температур атмосферного воздуха, получим расчетное выражение теплоты перегрева пара (кДж/кг):

В результате этих преобразований расчетное выражение энтальпии водяного пара при температуре t и давлении тройной точки воды Р₀ примет вид (кДж/кг)

Этим выражением можно пользоваться и для расчета энтальпий пара при давлениях, отличных от давления тройной точки воды. Это объясняется тем, что при атмосферных условиях парциальные давления пара малы и близки к давлению тройной точки воды. При Р_П>Р₀ (точка 2, рис.8.2) энтальпия пара будет представлять сумму трех слагаемых:

Энтальпии пара h_П соответствует площадь под изобарой Е-В-2. По сравнению с площадью под изобарой Е-1 здесь присутствует теплота q', но величины r и q_П уменьшились по сравнению с величинами r₀ и q_П1. При малых отклонениях изобар от изобары тройной точки воды в выражении h_П по сравнению с выражением для h_П1 будет происходить взаимная  компенсация уменьшения величин r и q_П за счет увеличения величины q'. В соответствии с рис. 8.2 эту взаимную компенсацию составляющих энтальпий h_П и h_П1 можно представить равенством площадей 11'2'D1 и 2DCЕВ2, т.е. будет справедливо равенство энтальпий h_П1 и h_П. На основании этого равенства получается расчетное выражение для энтальпии пара в атмосферном влажном воздухе:

(8.14)

Для определения энтальпии жидкой фазы воды принимают постоянной ее изобарную теплоемкость, что допустимо при параметрах атмосферного воздуха. Исходя из этого допущения расчетное выражение энтальпии жидкой фазы воды будет представлено в виде уравнения

(8.15)

Для определения энтальпии твердой фазы воды (лед, снег) принимаются постоянными удельная теплота плавления льда и его изобарная теплоемкость. Эти величины берутся при параметрах тройной точки воды. Такие допущения возможны, поскольку в соответствии с Р,t- диаграммой для воды (рис.8.3) имеют место следующие факты:

1) в атмосферном воздухе твердая фазы воды (т.ф.) может присутствовать только при температурах и парциальных давлениях пара, меньших (или равных) температуры и давления тройной точки воды, т.к. только на линии сублимации АС возможно одновременное существование паровой и твердой фаз воды;

2) плавление льда в атмосферном воздухе возможно только при температуре 0 ⁰С;

3) переход льда в паровую фазу при температурах меньше 0 ⁰С происходит, минуя жидкую фазу воды, - по линии сублимации (АС);

4) парциальное давление водяного пара при отрицательных температурах атмосферного воздуха не намного меньше (или равно) давления тройной точки воды Р₀, следовательно, теплота изобарного охлаждения твердой фазы воды от 0 ⁰С может быть рассчитана по изобаре Р₀.

Энтальпия льда будет величиной отрицательной, поскольку начало отсчета энтальпии идет от температуры 0 ⁰С жидкой фазы воды, а температура льда всегда меньше или равна 0 ⁰С. Расчетное выражение энтальпии твердой фазы воды (льда, снега) в атмосферном воздухе представляет собой сумму удельной теплоты плавления льда, взятой с отрицательным знаком, и удельной изобарной теплоты охлаждения льда от t=0 ⁰С до отрицательной температуры t:

(8.16)

В результате всех вышеприведенных упрощений окончательное расчетное выражение энтальпии влажного атмосферного воздуха (кДж/кг с.в.) примет вид

(8.17)