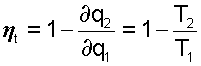
Ранее (раздел 4.1.4) было доказано, что энтропия идеального газа есть параметр состояния. Используя теорему Карно и учение об обратимых циклах, т.е. на базе второго закона термодинамики, можно доказать, что энтропия любого реального тела есть параметр состояния.

Для доказательства этого утверждения рассмотрим в Р,v- диаграмме произвольный внутренне обратимый (без трения) цикл (рис.9.14 а), который совершает реальное рабочее тело. При этом цикл может быть внешне необратимым, в данном случае, наличие разности температур между рабочим телом и источникам теплоты, роли не играют. Разобьем наш цикл, расположенными бесконечно близко друг к другу, адиабатами 14, 23, и т.д. на бесконечно большое количество элементарных циклов. Каждый из этих циклов можно считать циклом Карно, поскольку отрезки, полученные при делении цикла адиабатами, при бесконечно большом количестве последних можно считать изотермами, т.е. отрезок 12 и отрезок 34 заменить изотермами и т.д..

Совокупность этих элементарных циклов Карно эквивалентна нашему циклу, поскольку подведенная и отведенная теплота, а соответственно и работы циклов, будут одинаковы. Таким образом, наш цикл можно рассматривать как сумму бесконечного числа таких элементарных циклов Карно.

Для каждого элементарного цикла Карно, не зависимо от свойств рабочего тела, можно записать выражение термического КПД в виде

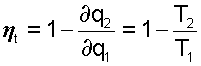где ∂q₁ и ∂q₂ - количество подведенной и отведенной теплоты;
Т₁ и Т₂ - температуры подвода и отвода теплоты цикла.
Из этого выражения получаются равенства

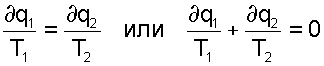при этом последнее выражение записано с учетом того, что отведенная теплота ∂q₂ не взята по модулю (как это сделано в выражении термического КПД), т.е. второе слагаемое этого выражения отрицательное.

Для совокупности всех элементарных циклов Карно, т.е. для всего замкнутого процесса, который совершает реальное рабочее тело можно записать выражение

(9.12)

что соответствует интегралу по замкнутому контуру для нашего цикла в виде.

(9.13)

Выражение (9.13) впервые было получено Клаузиусом и получило название интеграла Клаузиуса. Равенство нулю интеграла по замкнутому контуру свидетельствует о том, что под интегралом находится выражение полного диффиринциала. Выражение ∂q/T есть полный дифференциал энтропии, т.е. ∂q/T = ds, что позволяет записать выражение (9.13) в виде

(9.14)

Выражение (9.14) свидетельствует о том, что энтропия определяет состояние реального тела, т.е. она является параметром состояния любого реального тела. Следовательно, после этого доказательства принадлежности энтропии реальных тел к параметру состояния мы можем изобразить наш цикл в T,s- диаграмме (рис.9.14 б).

Понятия энтропии, связанной с механической, электрической или с любой энергией упорядоченного движения, в технической термодинамике не существует. Оно появляется только тогда, когда происходит превращение этих видов энергии в теплоту. То есть, есть теплота, есть и изменение энтропии. Являясь параметром состояния, энтропия, а точнее ее изменение, характеризует термодинамические процессы с точки зрения второго закона термодинамики.

Для обратимого процесса, используя первый закон термодинамики, изменение энтропии можно записать в виде выражения:

(9.15)

Для необратимого термодинамического процесса часть работы расширения за счет трения преобразуется в теплоту трения и усваивается телом. Поскольку в данном процессе будет присутствовать внешний и внутренний (за счет трения) подвод теплоты к телу, то и изменение энтропии (а, следовательно, и изменение термодинамического состояния тела) будет определяться как внешней теплотой, так и теплотой трения. Для необратимого термодинамического процесса изменение энтропии тела можно представить в виде выражения:

(9.16)

Поскольку в реальном необратимом процессе теплота трения всегда величина положительная ∂q_тр>0, то для необратимого процесса справедливо соотношение

(9.17)

Для обратимого процесса теплота трения отсутствует, что приводит к соотношению вида

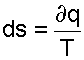(9.18)

Выражения (9.17) и (9.18) можно рассматривать как аналитические выражения второго закона термодинамики для тела, находящегося в замкнутой термодинамической системе.

Используя эти выражения, можно дать следующую формулировку второго закона термодинамики для тела - необратимость термодинамического процесса для тела приводит к увеличению изменения энтропии необратимого процесса по сравнению с изменением энтропии аналогичного обратимого процесса, при том же количестве подведенной внешней теплоты.

Такое увеличение энтропии тела для необратимого процесса, по сравнению с аналогичным обратимым, наглядно демонстрируется на примере адиабатных процессов (рис. 9.15).

Адиабатные процессы широко используются в технике - процессы расширения газа или пара в турбине, сжатия воды в насосе или газа в компрессоре. Для обратимых процессов ∂q=0 и ds=0, т.е. обратимая адиабата является изоэнтропой (процессы 12 и 34). В реальных адиабатных процессах всегда происходит увеличение энтропии, обусловленное наличием трения. Так, для необратимых адиабатных процессов 12* и 34* возрастание энтропии на величину s₂*-s₂ и s₄*-s₃ соответственно, обусловлено только теплотой трения этих процессов.

В связи с тем, что выражение ∂q* = Tds* отражает второй закон термодинамики, объединив его с первым законом термодинамики можно получить объединенное уравнение первого и второго законов термодинамики в виде выражений

(9.19)

(9.20)

где ds - изменение энтропии для любого процесса, как обратимого, так и для необратимого (звездочку при энтропии здесь не указывают).

Выражения (9.19) и (9.20) справедливы для любых процессов: обратимых и необратимых. Эти выражения используются для анализа термодинамических процессов и являются исходными для дифференциальных уравнений термодинамики в частных производных.