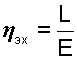
9.4.2.2.7. Методы оценки тепловой экономичности реальных циклов тепловых машин

При осуществлении любого реального необратимого цикла его работа всегда меньше эксергии источника теплоты. Отношение работы, полученной в цикле, к эксергии источника теплоты называется эксергетическим КПД.

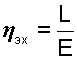(9.48)

Для полностью обратимого цикла эксергетический КПД равен единице. Для необратимого цикла эксергетический КПД показывает, какую долю потенциально возможной работы – эксергии – данного источника теплоты удалось преобразовать в полезную работу цикла.

Для примера, приведенного на рис.9.34, эксергетический КПД представляет отношение площадей:

Работу цикла можно представить в виде разности эксергии источника теплоты и ее потерь за счет необратимостей:

Метод оценки экономичности цикла тепловой машины посредством расчета потерь эксергии источника теплоты и определения эксергетического КПД цикла называется эксергетическим методом.

Этот метод позволяет детально оценить потери полезной работы во всех необратимых процессах цикла тепловой машины [5, 6].

Поскольку теорема Гюи–Стодолы -ΔE=T_ОСΔS_С представляет универсальное выражение для расчета потери эксергии в любом необратимом процессе, а увеличение эксергии системы за счет необратимостей процессов фактически определяет потерю эксергии, то величина ΔS_С выступает в роли оценки экономичности цикла тепловой машины. Метод оценки экономичности цикла тепловой машины, основанный на расчете увеличения энтропии системы за счет необратимостей реальных процессов, протекающих в цикле, называется энтропийным методом. Этот метод позволяет оценить, какую долю в общее увеличение энтропии системы вносит каждый необратимый процесс цикла тепловой машины. Анализ увеличения энтропии системы за счет каждого необратимого процесса и цикла в целом позволяет с помощью энтропийного метода проводить термодинамическую оптимизацию циклов тепловых машин. Для увеличения экономичности цикла необходимо стремиться к снижению увеличения энтропии системы и делать это целесообразно в тех процессах, где увеличение энтропии системы наибольшее.

На практике экономичность циклов тепловых машин оценивают с помощью метода теплового баланса с применением коэффициента использования теплоты, представляющего отношение работы цикла к полной теплоте внешнего источника:

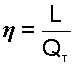(9.49)

В нашем примере величине Q_т соответствует площадь под процессом АВ, а L=пл.12341. Часть теплоты Q_Т не участвует в получении работы и выбрасывается в окружающую среду в виде теплоты уходящих газов Q_УХ (площадь под процессом DB). Другая часть теплоты Q_Т на процессе AD передается рабочему телу, которое совершает работу L и передает окружающей среде теплоту Q₂, соответствующую площади под процессом 43. Исходя из первого закона термодинамики, для нашей системы можно записать:

(9.50)

Выражение (9.50) получило название теплового баланса. В этом выражении величины Q_УХ и Q₂ представляют потери теплоты Q_Т в окружающую среду. Необходимо отметить, что потерь теплоты в окружающую среду в реальном цикле может быть больше: через поверхность парогенератора, регенеративные теплообменники и т.п.

Для нашего примера коэффициент использования теплоты можно представить выражением

(9.51)

В качестве использования этого выражения для оптимизации температуры уходящих газов Т_D и соответственно температуры подвода теплоты в цикл Карно Т₁ рассмотрим их влияние на потери теплоты в окружающую среду Q_УХ и Q₂ (рис.9.35).

Для упрощения анализа разность температур ΔТ=Т_D-Т₁ будем считать постоянной, т.е. в качестве переменной величины достаточно рассматривать только Т_D=Т_УХ. С увеличением Т_УХ от минимальной величины, равной Т_УХ.MIN=Т_ОС+ΔТ, до максимальной – Т_УХ.MAX=Т_A, потери теплоты с уходящими газами будут увеличиваться от Q_УХ=Q_УХ.MIN до Q_УХ.MAX=Q_Т, а потери теплоты от рабочего тела Q₂ будут уменьшаться от Q₂=Q_2MAX до Q_2MIN=0. Получается, что суммарные потери теплоты в окружающую среду Q_УХ+Q₂ имеют минимум. При минимальном значении суммы Q_УХ+Q₂, в соответствии с выражением (9.51), будет наибольший коэффициент использования теплоты нашего цикла. Следовательно, оптимальная температура уходящих газов будет соответствовать температуре Т_УХ.ОПТ на графике рис.9.35.

Аналогичную оптимизацию температуры уходящих газов можно выполнить на основании эксергетического или энтропийного метода. При этом в качестве критериев оптимального решения применяются величины минимальных потерь эксергии и минимального увеличения энтропии системы.

Все три метода оценки тепловой экономичности циклов тепловых машин имеют практическое применение. Метод теплового баланса наиболее простой, поэтому он широко используется в производственной практике. Эксергетический и энтропийный методы более трудоемкие в расчетной части, но они позволяют детально оценить любую необратимость каждого процесса и ее влияние на тепловую экономичность как всего теплового двигателя, так и отдельного его элемента. При этом можно выполнить расчет только отдельного необратимого процесса для оценки его необратимости, что невозможно в методе теплового баланса, который требует полного расчета всего цикла теплового двигателя. Кроме этого, балансовый метод может дать максимальную величину коэффициента использования теплоты (даже равного единице) при нулевом значении работы цикла (цикл ГТУ, цикл противодавленческой ПТУ), что делает его в этом случае непригодным для оценки экономичности тепловой машины. О таких ситуациях подробно рассказано в [1, 5, 6].

На основании вышеизложенного, эксергетический и энтропийный методы имеют практическое применение в теплоэнергетике в следующих случаях:

3) при проведения оптимизации параметров рабочих тел и выборе оптимальных схем и циклов тепловых машин.