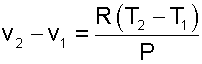
На рис.5.2 изображены характерные политропные процессы в Р,v- координатах. Все процессы проведены через общую точку А, что позволяет наглядно сопоставить изображение политроп с различными значениями показателя политропы n.
Показатель политропы определяет характер процесса. В Р,v- координатах политропа описывается уравнением Рvn=const, в соответствии с которым основные процессы будут представлять:
изобара - горизонтальная прямая, n=0, Р=const;
изохора - вертикальная прямая, n=±∞, v=const;
изотерма - равнобокая гипербола с осями асимптот в виде осей координат Р и v, т.к. при n=1 уравнение изотермы pv=const, а константа величина положительная;
адиабата - неравнобокая гипербола, т.к. при n=к>1 уравнение адиабаты Рvk=const, адиабата круче изотермы.
Политропы при 0 < n < +∞ в соответствии с уравнением Р/vn=const представляют собой гиперболы, крутизна которых возрастает с увеличением показателя n. Самая крутая из них изохора (n=∞), а самая пологая - изобара (n=0). Все политропы с положительным показателем n>0 располагаются во II и IV квадрантах относительно точки А.
Политропы с 1 < n < к располагаются между изотермой и изоэнтропой (s=const) и имеют отрицательную теплоемкость в соответствии с уравнением (5.9). В таких процессах при подводе теплоты температура газа уменьшается, а при отводе теплоты от газа его температура увеличивается. Примером такого процесса может служить сжатие газа (l<0) в цилинре с поршнем при его внешнем охлаждении (q<0), когда величина работы сжатия по модулю больше величины, отведеной от газа теплоты |l|>|q|, т.е. в этом случае будет увеличение внутренней энергии (Δu=q-l>0) и температуры газа при отводе от него теплоты.
n = -1 - это прямая линия,
-1 < n < 0 - кривая выпуклостью вверх,
-∞ < n < -1 - кривая выпуклостью вниз.
При n=-1 теплоемкость процесса имеет среднее арифметическое значеие между изобарной и изохорной теплоемкостями с=(cp+cv)/2. Все политропы с отрицательным показателем n<0 располагаются в I и III квадрантах относительно точки А. В диаграмме P,v изотермы, а так же адиабаты, идеального газа представляют собой не пересекающиеся гиперболы (рис.5.3). Однако они не являются эквидистантными кривыми, поскольку расстояние между ними по оси v будет изменяться в зависимости от численного значения давления. Так для двух изотерм Т1=const и Т2=const расстояние по оси v будет определяться по изобаре P=const выражением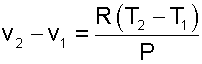 |
В соответсвии с этим выражением при увеличении давления расстояние между двумя изотермами по оси v уменьшается, если Т2>Т1. Кроме этого, исходя из уравнения изобары Т2/Т1=v2/v1, изотермы в P,v- диаграмме находятся одна над другой (или одна правее другой) по возрастающей, т.к. Т2>T1 только при v2>v1.
Для двух адиабат s1=const и s2=const расстояние между ними по оси v можно оценить по любой изобаре P=const. Исходя из уравнений адиабатного и изобарного процессов
 |
следует, что точке на данной изобаре с большим объемом будет соответствовать большее значение энтропии, т.е. при v2>v1 будет s2>s1. Следовательно, в Р,v- диаграмме адиабаты-изоэнтропы, чем выше (или правее), тем большее значение энтропии им соответствует.
Для изоэнтропы s2 в уравнении PvK=const=А2 константа А2 будет больше, чем константа А1 изоэнтопы s1 в уравнении PvK=const=А1. Поскольку при Р=const Pv2K-Pv1K=А2-А1>0. Выразив объем из уравнения адиабаты v=const/P1/K, получим расстояние между двумя адиабатами вдоль оси v в виде выражения
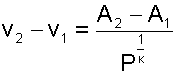 |
Из этого выражения видно, что с увеличением давления расстояние между адиабатами вдоль оси v в P,v- диаграмме уменьшается, т.е. адиабаты в Р,v- диаграмме не являются эквидистантными кривыми, хотя на всем своем протяжении не пересекаются друг с другом.
Для политропного процесса идеального газа изменение энтропии определяется уравнением (5.13)
 |
Изображение политропы в Т,s- диаграмме ведется в соответствии с этим уравнением при фиксации начала отсчета энтропии.
В общем случае начало отсчета энтропии sO=0 можно зафиксировать любой парой независимых параметров состояния. Для упрощения анализа политропы зафиксируем sO=0 точкой, находящейся на нашей политропе при температуре ТO. В этом случае второй параметр состояния, определяющий sO=0, при расчете абсолютного значения энтропии не потребуется, т.к. он определен своим местом нахождения на данной политропе. При необходимости его несложно определить через параметры любой точки на данной политропе, воспользовавшись одним из уравнений политропы, включающим температуру, например,
Таким образом, расчетное выражение абсолютного значения энтропии можно представить в виде
 |
(5.31) |
Выражение (5.31) соответствует логарифмической кривой. При положительной теплоемкости c>0 эта кривая в s,T- координатах изображена на рис. 5.4 а. Та же кривая в Т,s- кординатах (перевернутых) показана на рис. 5.4 б. Таким образом, в Т,s- кординатах политропа представляет лагорифмическую кривую.
а)............................................б) Рис. 5.4. Изображение политропы в T,s- диаграмме |
Политропа с отрицательной теплоемкостью представляет собой лагорифмику в виде зеркального отражения политропы с такой же, но положительной теплоемкостью, относительно оси Т (рис.5.5).
Причем, если подкасательная любой точки политропы (подкасательная в Т,s- кординатах соответствует теплоемкости данной точки процесса) расположена слева от нее, то теплоемкость этой политропы положительная c>0, если подкасательная расположена справа от точки - теплоемкость политропы отрицательная с<0 (рис.5.5).
Численное значение теплоемкости политропы определяет ее крутизну в Т, s- диаграмме. Чем больше теплоемкость, тем больше подкасательная и меньше крутизна политропы.
Характер основных политропных процессов в Т,s- диаграмме показан на рис.5.6. Для наглядности сопоставления характера политропных процессов они проведены через общую точку А.
Политропы, проходящие через I и III квадранты, относительно точки А имеют положительную теплоемкость, причем изохора круче изобары, т.к. cP > cV. Самая крутая политропа - адиабата, для нее теплоемкость равна нулю. Самая пологая политропа - изотерма, для нее теплоемкость равна бесконечности.
Политропы, проходящие через II и IV квадранты, имеют отрицательную теплоемкость.
Процессы идеальных газов с одинаковыми показателями политропы в T,s- диаграмме представляют собой эквидистантные по оси s кривые (непересекающиеся, с одинаковым расстоянием друг от друга по оси s). На рис.5.7 изображены в Т,s- диаграмме две политропы идеального газа А1А2 и В1В2 с одинаковым показателем n и, соответственно, с одинаковыми теплоемкостями.
Рис. 5.7. К доказательству эквидистантности политроп с одинаковыми показателями n....................................... |
Доказать, что эти политропы эквидистантны несложно. Достаточно рассмотреть расстояние между ними вдоль оси s по двум произвольным изотермам Т1 и Т2. Поскольку теплоемкости этих процессов одинаковые, то изменение энропии на интервале температур Т1-Т2 в этих процессах тоже одинаковое и соответствует отрезкам
 |
В прямоугольнике С1А2В2С2 противоположные стороны равны А2В2=С1С2, равны и отрезки А1С1 = В1С2, следовательно, равны и отрезки А1В1=А2В2. Расстояние между этими политропами по иси s можно расчитать по формуле оределения изменения энтропии изотермического процесса (5.13) при любой температуре
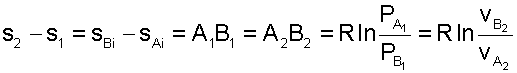 |
Изобарры и изохоры являются частными случаями политроп, следовательно, и они представляют в Т,s- диаграмме эквидистантные по оси s кривые. В Т,s- координатах (рис.5.8) изобары находятся одна над другой по возрастающей, а изохоры одна под другой по возрастающей, т.к., если брать расстояние между ними по изотерме, оно будет равно положительной разности энтропий
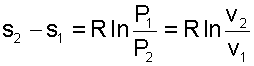 |
Рис. 5.8. Относительное расположение изобар и изохор в T,s- диаграмме: P1>P2, V 1<V2.......................................... |
| предыдущий параграф | содержание | следующий параграф |