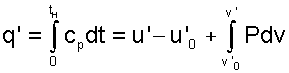
(7.4)
В теплоэнергетических установках вода используется в двух фазовых состояниях: в виде пара и жидкости. Поэтому в дальнейшем будем рассматривать только эти две фазы воды.
В технических расчетах абсолютные величины энергетических параметров (энтропия, внутренняя энергия, энтальпия) не имеют принципиального значения. Поэтому допустима свобода выбора начала отсчета этих параметров. Необходимо, конечно, учитывать аналитические связи этих величин между собой и с другими терм0 и t0, взятых за начало отсчета для u0, будут разными числами (h0>u0).
Для воды в качестве опорной точки принята тройная точка [11]. При давлении и температуре тройной точки Р0 = 611,2 Па и Т0 = 273,16 К приняты равными нулю энтропия и внутренняя энергия жидкой фазы воды (на линии х=0), соответствующее этим параметрам значение энтальпии h'0=0,614 Дж/кг (это энтальпия на линии х=0). Все параметры на линии насыщения жидкой фазы воды обозначаются с одним штрихом.
При давлениях, применяемых в технических устройствах, жидкость можно считать несжимаемой, т.е. с постоянным объемом, не зависящим от давления. Следовательно, расстояние между молекулами жидкости будет зависеть только от температуры, а внутренняя энергия жидкости будет функцией только одного параметра - температуры, т.к. кинетическая и потенциальная ее составляющие определяются только температурой. Таким образом, с достаточной степенью точности для технических расчетов можно считать, что при 0 0С (273,15 К) внутренняя энергия жидкости, независимо от давления, равна нулю. Здесь отождествляется t=0 0С с температурой тройной точки воды, а изотерма при t=0 0С в области жидкой фазы будет выступать в качестве левой пограничной кривой жидкой фазы.
Рассмотрим процесс нагрева жидкости от нулевой температуры до температуры насыщения при заданном давлении Р=const в Р,v- и T,s- диаграммах (рис. 7.10 и 7.11). Целью анализа этого процесса будет представление методики определения энергетических параметров жидкости на линии насыщения х=0 и ее изобарной теплоемкости: h', u', s', cР'. Экспериментально можно определить только зависимость температуры, давления и удельного объема друг от друга, а также замерить количество теплоты процесса. Поэтому энергетические параметры и теплоемкость процесса являются расчетными величинами.
Для нагрева жидкости от t=0 0С до температуры насыщения tН при заданном давлении Р (процесс 1-2) ей нужно сообщить количество теплоты
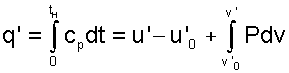 |
(7.4) |
Все величины в выражении (7.4) взяты на линии насыщения х=0.
Нагрев жидкости от t=0 0С до tН, соответствующей давлению Р, можно осуществить по изобаре 1-2 и по линии 1-М-2 (рис. 7.10) в Р,v- диаграмме, а в T,s- диаграмме (рис. 7.11) точки 1 и М совместятся и процесс 1-М-2 пойдет по пограничной кривой х = 0. В обоих случаях изменение внутренней энергии одно и то же, а работа расширения процесса 1-2 отличается от работы расширения процесса 1-М-2 на заштрихованную площадь 12М1 в Р,v- диаграмме. Разница в затратах теплоты, при нагреве жидкости по изобаре и по пограничной кривой x = 0 (рис. 7.11), обусловлена разностью работ. Эта разница работ составляет практически неощутимую величину, т.к. работа изменения объема очень мала по сравнению с изменением внутренней энергии жидкости (объем жидкости меняется очень незначительно). Так, при давлении 20 бар при нагреве жидкости от t = 0 0С до tН = =212,37 0С общая затрата теплоты составляет 906,6 кДж/кг, а на долю работы расширения приходится 0,355 кДж/кг, т.е. менее 0,04 %. Следовательно, нагрев жидкости в основном определяется изменением внутренней энергии, которое зависит практически только от изменения температуры.
Исходя из сказанного теплоемкость жидкости сp=dq'/dt в основном зависит от температуры, и зачастую в инженерных расчетах она принимается как функция только одного параметра - температуры. Это подтверждается и экспериментальными данными, так при t=90 0С удельная изобарная теплоемкость жидкости при давлении 1 бар равна 4,205 кДж/(кг К), а при давлении 50 бар - 4,194 кДж/(кг К), что соответствует 0,26 % относительной разности этих теплоемкостей.
Количество теплоты q', затраченное на нагрев 1 кг жидкости от t=0 0С до tН при заданном постоянном давлении, называется теплотой жидкости. Так как это теплота изобарного процесса - она соответствует разности энтальпий:
(7.5) |
Поскольку h0 = u0 + Рv0, а u0=u'0=0 и v'0=v0 (при всех давлениях жидкости), равенство (7.5) можно записать как
(7.6) |
Величина Рv0' очень мала по отношению к q', и при невысоких давлениях можно принимать q' @ h'. Внутренняя энергия жидкости на линии насыщения рассчитывается по энтальпии
(7.7) |
Исходя из выражений (7.6) и (7.7) и того, что v'>v0', получим соотношение h'>q'>u'. При небольших давлениях (до 100 бар) разница между этими тремя величинами h', q', u' очень мала. Например, при давлении 100 бар эта разница не превышает 10 кДж/кг.
Исходя из вышеизложенного энтальпию жидкости на линии насыщения х=0 можно определить как сумму h'=q'+Рv0'. В свою очередь, теплоту жидкости q' определяют экспериментально или рассчитывают по заранее определенной зависимости изобарной теплоемкости жидкости от температуры при заданном давлении. При давлениях до 10 бар изобарная теплоемкость жидкости мало зависит от температуры и давления и в приближенных расчетах может приниматься постоянной и равной 1 ккал/(кг К) или 4,187 кДж/(кг К).
Энтропия жидкости на линии насыщения x = 0 определяется исходя из принятого условия ее равенства нулю в тройной точке воды (s0'=0). С изменением давления энтропия жидкости при температуре тройной точки (или 0 0С) s0 изменяется, однако это изменение очень незначительное. Поскольку энтропия, как любой параметр состояния, является функцией двух независимых параметров состояния, а при t=0 0С для всех давлений жидкости внутренняя энергия жидкости практически равна нулю, то и энтропия жидкости при t=0 0С для всех давлений будет практически постоянной и равной энтропии жидкости в тройной точке воды, т.е. s0=0. Так при давлении 22 МПа и t=0 0С s0=0,0009 кДж/(кг К), а при давлении 1 кПа энтропия жидкости на линии насыщения s'=0,106 кДж/(кг К), т.е. энтропия жидкости при t=0 0С несоизмеримо мала по сравнению с энтропией жидкости в состоянии насыщения для всех давлений, используемых в практической деятельности.
Зная значение энтропии s0 при t=0 0С и заданном давлении, энтропию жидкости на линии насыщения при TН можно определить как
 |
(7.8) |
где s0 = s0'= 0 – при давлениях, используемых в технике;
сР = 4,187 кДж/(кг•К) – при умеренных давлениях (до 150 бар).
В точных расчетах надо пользоваться средней изобарной теплоемкостью воды в данном интервале температур.
В соответствии с выражением (7.8) процесс изобарного нагрева жидкости от t= 0 0С до ТН начинается в точке 1 в T,s- диаграмме при всех давлениях и представляется логарифмической кривой 12, идущей выше линии x = 0 (см. рис. 7.11). Площадь под кривой 12 соответствует теплоте жидкости q'. При этом линии 12 и x = 0 очень близки друг к другу, что позволяет с достаточной точностью в области жидкости изобары с умеренными значениями давлений воспринимать как линию x=0 от t=0 0С до ТН.
Определение энтальпии, энтропии и внутренней энергии жидкости при температурах меньших, чем температура насыщения при заданном давлении, ведется аналогичным образом.
| предыдущий параграф | содержание | следующий параграф |